月球軌道
月球軌道以27.323天完整的環繞地球一圈。地球和月球的質心在距離地心4,700公里處(地球赤道半徑的⅔),兩者各自圍繞著質心運轉。月球與地球中心的平均距離是385,000公里,大約是地球半徑的60倍。軌道的平均速度是1.023公里/秒,月球在恆星的背景之間大約每小時移動0.5°,這相當於月球的視直徑。月球的軌道不同於大部分行星的天然衛星,它是接近黃道平面,而非地球的赤道平面。月球軌道面相對於黃道平面的傾斜只有5.1°,自轉軸的傾角也只有1.5°。
月球繞行地球的軌道大小和距離的比例。圖片中一個畫素寬度對應至實際上500公里的距離
目录
1 月球軌道的特性
2 月球的月
3 月球軌道的潮汐演變
4 天秤動
5 月球停變期
6 月球和地球環繞太陽的路徑
7 相關條目
8 參考資料
月球軌道的特性

軌道參數的定義。
| 性質 | 數值 |
|---|---|
| 半長軸 | ~384 748 公里 |
| 近地點距離 | ~364 397 公里 |
| 遠地點距離 | ~406 731 公里 |
| 平均離心率 | 0.0549006 (0.044 – 0.067) |
| 平均轉軸傾角 | 6.688° |
| 平均軌道傾角(對黃道) | 5.145° |
| 平均軌道傾角(赤道對黃道) | 1.543° |
交點退行週期 | 18.5996 年 |
| 拱點線退行週期 | 8.8504 年 |

近點月和遠點月的大小比較。
月球的质心和地球的质心長期的平均距離大約是385,000 公里,相當於地球半徑的60倍,或是地球直徑的30倍。兩者共同的質心大約離地球中心4,670公里,也就是在地表下約1,700 公里。與太陽系內其他行星的天然衛星比較,地月大小的比例(4:1)是相對的大,而地月質量的比例是較小的(81:1),因此有些人認為地月系統應該是雙行星。但是,雙行星有個不成文的定義,即雙行星的質心應該在兩個行星的外部,而不應該在兩者的任何一顆之中,所以地月系統還是一個普通的行星與衛星的系統。
月球軌道的平均離心率是0.0549。非圓形的軌道導致從地球上觀察月時,視直徑的大小和角速度上都有著明顯的改變。對一位虛構的在質心上的觀測者而言,月球每天的平均角位移量是向東13. 176358°,軌道的指向在空間中並沒有被固定住,而是隨著時間不斷的進動,其中一種是拱點線的進動:橢圓形的月球軌道慢慢的反時針方向轉動,完整的旋轉一圈是8.850年(3,233天)。另一種運動是軌道平面本身的軸垂直於黃道的順時針進動。月球軌道與黃道的交點對時間的進動,完整的環繞一圈是18.6年(6,793天)。
月球軌道對黃道平面的傾角是5.145°。月球的自轉軸並沒有垂直於公轉的軌道平面,所以月球赤道相對於軌道平面的傾角常數是6.688°。或許曾有人試圖由月球軌道平面的進動,去解釋月球赤道和黃道之間的傾角應該始終在這兩個數值的合(11.833°)和差(1.543°)之間變化者。不過,在1721年賈可·卡西尼已經解決了這個問題,因為月球進動軸的旋轉與軌道平面有相同的速率,但是相位相差180°(參見卡西尼定律)。因此,雖然月球的自轉軸相對於恆星並沒有固定,但是月球的赤道平面和黃道始終保持著在1.543°。
月球的月
月球的週期 |
| 名稱 | 數值(天) | 定義 |
|---|---|---|
| 恆星月 | 27.321 661 | 相對於遙遠的恆星(每年13.369個恆星月) |
| 朔望月 | 29.530 589 | 相對於太陽(月球的相位,每年12.369 朔望月) |
| 分至月 | 27.321 582 | 相對於春分點(進動 ~ 26,000儒略年) |
| 近點月 | 27.554 550 | 相對於近地點(recesses in 3232.6 天 = 8.8504 儒略年) |
| 交點月 | 27.212 221 | 相對於昇交點(進動週期 6793.5 天 = 18.5996 儒略年) |
有許多種不同的方法可以定義月球完成一個軌道週期。恆星月是相對於遙遠的恆星,大約是27.32天。在對照上,朔望月是月球回到原來月相的時間,大約是29.53天。朔望月比恆星月長,是因為地月系統在有限的距離內繞者太陽運轉,在經歷一個恆星月的時間之後,還要更多的時間才能回到原來的幾何對應位置。其他的定義還有從近地點至近地點(近點月)、從昇交點再回到昇交點(交點月)和在黃道座標上再回到相同黃經(分至月)。由於緩慢的進動造成的影響,後面這三個月的長度都和恆星月有些微的差距,而曆年的月長度大約是30.4天(1/12年)。
月球軌道的潮汐演變
月球施加於地球的萬有引力是造成洋發生潮汐的起因。如果地球的海洋擁有全球一致的深度,月球將會使固體的地球(只有極小的改變量)和海洋都變型成為橢球型,最高點就直接出現在朝向月球和背對月球的一點。但是因為地球有著不規則的海岸線和多變化的海洋深度,就只能想像這種理想狀態了。一般來說,潮流的漲落週期與月球環繞地球的軌道週期同步,但會隨著月相變化。雖然很罕見,但在地球上有些地區每天只有一次的潮汐漲落。
由於地球的自轉,潮汐的突起會略為超前地月系統的軸線一些,這是海水在海底的移動和在海灣的出海口進出造成摩擦和能量散逸的直接結果。每個凸出部份都會對月球施加少量的引力,因為地球帶動這凸出物向前運動,與月球最接近的凸起部分會沿著月球軌道輕微的拉扯月球向前;背向月球那一側的凸起物則產生相反的效應。但是較靠近月球的凸起物因為距離較近,對月球的影響也較大,因此結果是地球的轉動慣量逐漸的轉移到月球軌道的轉動慣量。這使得月球的軌道慢慢的逐漸遠離地球,每年移動的量大約是3.8公分。為了維持角動量守恆,地球的轉速正逐漸減慢,使得地球的一天每年延長約17微秒(這個數字會使地球日每60,000年增加一秒鐘,每400萬年增加一分鐘,十億年增加4小時。往回推算,當6,500萬年前恐龍在地球上出沒時,一天的長度是23小時。)。參考潮汐加速有更詳細的說明和參考資料。
所以月球正逐漸遠離地球,並進入較高的軌道中,而依據計算(根據NASA和噴射推進實驗室 (JPL)[1])認為這個過程將再持續大約20億年。屆時,地球和月球的軌道將成為"自轉–軌道共振",月球大約每47天繞地球公轉一圈(目前是27.32天),並且地球和月球的自轉也是相同的這個週期,即兩者始終以相同的一面互相環繞者。除此之外,很難說地月系統還會發生什麼樣的改變
天秤動
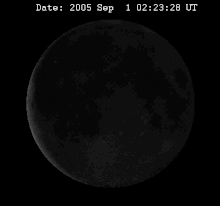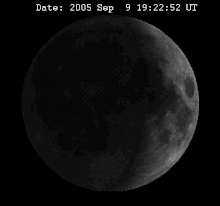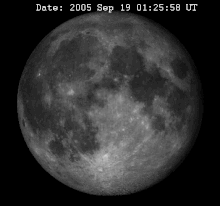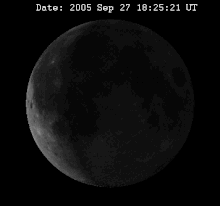
月球相位變化的動畫。視覺上的擺動就是所謂的天秤動。
月球是同步自轉,意味著它永遠以同一面朝向地球轉動著,但因為月球軌道的離心率 (事實上這也只是一種平均的現象),使環繞地球的軌道角速度會變化,因而不能與不變的自轉速度相等的結果。當月球在近地點時,它的自轉速相對於軌道速度是最慢的,這使得我們可以看見偏東(右邊)達到8度的經度的背面區域。反過來,當月球在遠地點時,它的自轉相對於軌道速度是最快的,因此可以看見背面偏西8度的經度。這就是經度天秤動。
因為月球軌道對地球運行的黃道傾斜5.1°,所以軌道的自轉軸再環繞地球一周時會朝向與遠離地球,這種變化稱為緯度天秤動,可以在緯度上跨越極區,在兩極各看見背面7°的區域。最後,因為月球與地球的距離只有60倍的地球半徑,造成周日天秤動可以在經度上再多看一度的區域。同樣的理由,由兩極的視差也可以多看緯度的一度。
月球停變期
當月球軌道的升交點,剛好在北半球的春分點時,月球在天空中的赤緯會達到最大值的23°29′ + 5°9′或 28°36′,這被稱為最大停變期。9年半以後,當月球的降交點來到相同的位置時,角度將僅有23°28′ − 5°8′或18°19′,月球的赤緯是最低的,這稱為最小停變期。
月球和地球環繞太陽的路徑


灰色为月球轨道,蓝色为地球轨道,太阳位于图像左下方。可以看出月球绕日的轨道永远是凹向的。
人们在描述太陽系時,總是將地球描述成在軌道上環繞太陽的一個點,月球則是在軌道上環繞地球的一個點。這可能會給人月球是繞著地球運轉的概念,但從太陽的位置觀察時,月球则也是绕着太阳运动,只是其有时會落後或超前于地球。因為相對於地球每秒30公里的绕日速度,月球绕地球每秒1公里的軌道速度是不容易察覺的。
不同於太陽系其他的衛星,完整的月球軌道與地球的非常相似,其凹面也永遠朝向太陽,並且沒有凸起或環圈[2][3]。这并不能說月球是繞著太陽轉而不是繞著地球,因為即使將太陽的引力消失,月球還是會以和現在相同的恆星月繞著地球。如果地月系統離太陽更遠或地球离月球更近,在該處的軌道速度就有可能低於1公里/秒,則在以太陽為中心的非轉動座標系統中,月球的運動就會出現逆行的現象。
相關條目
- Ernest William Brown
- 月相
- 月球停變期
- 軌道根數
- 進動
- 軌道列表
- 轉軸傾角
- 米蘭科維奇循環
- Astrological age
- 大年
- 軌道離心率
- 晝夜平分點
- 近地點
參考資料
^
Dickinson, Terence. From the Big Bang to Planet X. Camden East, Ontario: Camden House. 1993: 79–81. ISBN 0-921820-71-2.
^ The Orbit of the Moon around the Sun is Convex!. [2006-04-21].
^ Vacher, H.L. Computational Geology 18 - Definition and the Concept of Set (PDF). Journal of Geoscience Education. Nov 2001, 49 (5): 470–479 [2006-04-21].
| ||||||||||
| |||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||














