Agfdhyk

在這篇文章內，向量與标量分別用粗體與斜體顯示。例如，位置向量通常用 r{displaystyle mathbf {r} ,!} 表示；而其大小則用 r{displaystyle r,!} 來表示。

圖1 - 紅色的圓圈，半徑是2，圓心位於直角座標系的原點。此圓的方程為x2+y2=4{displaystyle x^{2}+y^{2}=4}。

在數學裏，笛卡兒坐標系（英语：Cartesian coordinate system），也稱直角坐標系，是一種正交坐標系。參閱圖1，二維的直角坐標系是由兩條相互垂直、相交於原點的數線構成的。在平面內，任何一點的坐標是根據數軸上對應的點的座標設定的。在平面內，任何一點與坐標的對應關係，類似於數軸上點與坐標的對應關係。

採用直角坐標，幾何形狀可以用代數公式明確的表達出來。幾何形狀的每一個點的直角坐標必須遵守這代數公式。例如：直線可以標準式ax+by+c=0{displaystyle ax+by+c=0}、斜截式y=mx+k{displaystyle y=mx+k}等式子來表示;一個圓，半徑為r，圓心位於(a,b)。圓圈可以用以(x−a)2+(y−b)2=r2{displaystyle (x-a)^{2}+(y-b)^{2}=r^{2}}表示。

歷史

笛卡尔坐標系是由法國數學家勒內·笛卡尔創建的。1637年，笛卡尔發表了巨作《方法論》。這本專門研究與討論西方治學方法的書，提供了許多正確的見解與良好的建議，對於後來的西方學術發展，有很大的貢獻。為了顯示新方法的優點與果效，以及對他個人在科學研究方面的幫助，在《方法論》的附錄中，他增添了另外一本書《幾何》。有關笛卡兒坐標系的研究，就是出現於《幾何》這本書內。笛卡兒在坐標系這方面的研究結合了代數與歐幾里得幾何，對於後來解析幾何、微積分、與地圖學的建樹，具有關鍵的開導力。

二維坐標系統

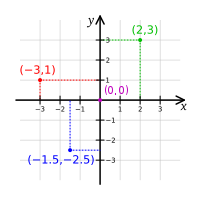
圖2 - 直角坐標系。圖中四點的坐標分別為，綠點：(2, 3){displaystyle (2, 3)}，紅點：(−3, 1){displaystyle (-3, 1)}，藍點：(−1.5, −2.5){displaystyle (-1.5, -2.5)}，紫點：(0, 0){displaystyle (0, 0)}。

圖3 - 直角坐標系的四個象限，按照逆時針方向，從象限I{displaystyle I}到象限IV{displaystyle IV}。坐標軸的頭部象徵著，往所指的方向，無限的延伸。

參閱圖2，二維的直角坐標系通常由兩個互相垂直的坐標軸設定，通常分別稱為x-軸和 y-軸；兩個坐標軸的相交點，稱為原點，通常標記為O，既有「零」的意思，又是英語「Origin」的首字母。每一個軸都指向一個特定的方向。這兩個不同線的坐標軸，決定了一個平面，稱為xy-平面，又稱為笛卡兒平面。通常兩個坐標軸只要互相垂直，其指向何方對於分析問題是没有影響的，但習慣性地（見右圖），x-軸被水平擺放，稱為橫軸，通常指向右方；y-軸被豎直擺放而稱為縱軸，通常指向上方。兩個坐標軸這樣的位置關係，稱為二維的右手坐標系，或右手系。如果把這個右手系畫在一張透明紙片上，則在平面內無論怎樣旋轉它，所得到的都叫做右手系；但如果把紙片翻轉，其背面看到的坐標系則稱為「左手系」。這和照鏡子時左右對調的性質有關。

為了要知道坐標軸的任何一點，離原點的距離。假設，我們可以刻畫數值於坐標軸。那麼，從原點開始，往坐標軸所指的方向，每隔一個單位長度，就刻畫數值於坐標軸。這數值是刻畫的次數，也是離原點的正值整數距離；同樣地，背著坐標軸所指的方向，我們也可以刻畫出離原點的負值整數距離。稱x-軸刻畫的數值為x-坐標，又稱横坐標，稱y-軸刻畫的數值為y-坐標，又稱縱坐標。雖然，在這裏，這兩個坐標都是整數，對應於坐標軸特定的點。按照比例，我們可以推廣至實數坐標和其所對應的坐標軸的每一個點。這兩個坐標就是直角坐標系的直角坐標，標記為(x, y){displaystyle (x, y)}。

任何一個點P在平面的位置，可以用直角坐標來獨特表達。只要從點P畫一條垂直於x-軸的直線。從這條直線與x-軸的相交點，可以找到點P的x-坐標。同樣地，可以找到點P的y-坐標。這樣，我們可以得到點P的直角坐標。例如，參閱圖3，點P的直角坐標是(3, 5){displaystyle (3, 5)}。

直角坐標系也可以推廣至三維空間與高維空間 (higher dimension)。

參閱圖3，直角坐標系的兩個坐標軸將平面分成了四個部分，稱為象限，分別用羅馬數字編號為I (+, +){displaystyle I (+, +)}，II (−, +){displaystyle II (-, +)}，III (−, −){displaystyle III (-, -)}，IV (+, −){displaystyle IV (+, -)}。依照慣例，象限I{displaystyle I}的兩個坐標都是正值；象限II{displaystyle II}的x-坐標是負值，y-坐標是正值；象限III{displaystyle III}的兩個坐標都是負值的；象限IV{displaystyle IV}的x-坐標是正值，y-坐標是負值。所以，象限的編號是按照逆時針方向，從象限I{displaystyle I}編到象限IV{displaystyle IV}。

三維坐標系統

圖4 - 直角坐標系的幾個坐標曲面。紅色平面的x=1{displaystyle x=1}。黃色平面的y=−1{displaystyle y=-1}。藍色平面的z=1{displaystyle z=1}。z-軸是竖直的，以白色表示。x-軸以綠色表示。三個坐標曲面相交於點P（以黑色的圓球表示），直角坐標大約為(1, −1, 1){displaystyle (1, -1, 1)}。

圖5 - 三維直角坐標系。y-軸的方向是遠離讀者。

在原本的二維直角坐標系，再添加一個垂直於x-軸，y-軸的坐標軸，稱為z-軸。假若，這三個坐標軸滿足右手定則，則可得到三維的直角坐標系。這z-軸與x-軸，y-軸相互正交於原點。在三維空間的任何一點P，可以用直角坐標(x, y, z){displaystyle (x, y, z)}來表達其位置。例如，參閱圖5，兩個點P與Q的直角坐標分別為(3, 0, 5){displaystyle (3, 0, 5)}與(−5, −5, 7){displaystyle (-5, -5, 7)}。

三個平面，xy-平面，yz-平面，xz-平面，將三維空間分成了八個部分，稱為卦限 (octant)。與二維空間的四個象限不同，只有一個卦限有編號。第一號卦限的每一個點的三個坐標都是正值的。

取向

二維空間

直角坐標系的x-軸與y-軸必須相互垂直。稱包含y-軸的直線為y-線。在二維空間裏，當我們設定了x-軸的位置與方向的同時，我們也設定了y-線的方向。可是，我們仍舊必須選擇，在y-線的以原點為共同點的兩條半線中，那一條半線的點的坐標是正值的，那一條是負值的？任何一種選擇決定了xy-平面的取向。

參閱圖1。通常，我們選擇的取向是，正值的x-軸横地指向右方，正值的y-軸縱地指向上方。這種取向稱為正值取向，標準取向，或右手取向。

右手定則是一種常用的記憶方法，專門用來辨認正值取向：將一隻半握拳的右手放在平面上，大拇指往上指，那麼，其它的手指都從x-軸指向y-軸。

另外一種取向，採用左手定則，專門用來辨認負值取向，或左手取向：將一隻半握拳的左手放在xy-平面上，大拇指往上指，那麼，其它的手指都從y-軸指向x-軸。

不論坐標軸是何種取向，將坐標系統做任何角度的旋轉，取向仍舊會保持不變。

三維空間

圖8 –左邊是左手取向，右邊是右手取向。

直角坐標系的x-軸，y-軸，與z-軸必須相互垂直。稱包含z-軸的直線為z-線。在三維空間裏，當我們設定了x-軸，y-軸的位置與方向的同時，我們也設定了z-線的方向。可是，我們仍舊必須選擇，在z-線以原點為共同點的兩條半線中，哪一條半線的點的坐標是正值的，哪一條是負值的？這兩種不同的坐標系統，稱為右手坐標系與左手坐標系。右手坐標系又稱為標準坐標系，或正值坐標系。

右手坐標系這名詞是由右手定則而來的。先將右手的手掌與手指伸直。然後，將中指指向往手掌的掌面半空間，與食指呈直角關係。再將大拇指往上指去，與中指，食指都呈直角關係。則大拇指，食指，與中指分別表示了右手坐標系的x-軸，y-軸，與z-軸。同樣地，用左手也可以表示出左手坐標系。

圖8試著展示出一個左手坐標系與一個右手坐標系。因為我們用二維畫面來展示三維物體，會造成扭曲或模稜兩可的圖形。指向下方與右方的軸，也有指向讀者的意思；而位置居於中間的軸，也有指向讀者正在看的方向的意思。平行於xy-平面的紅色圓形曲箭，其紅色箭頭從z-軸前面經過，表示從x-軸往y-軸的旋轉方向。

向量

採用直角坐標系，在三維空間裏，任何一點P都可以用向量來表示。我們可以想像向量為一支羽箭，其箭尾在原點，箭鋒在點P。假若點P的向量是r{displaystyle mathbf {r} }，直角坐標是(x,y,z){displaystyle (x,y,z)}。那麼，

r=xi^+yj^+zk^{displaystyle mathbf {r} =x{hat {mathbf {i} }}+y{hat {mathbf {j} }}+z{hat {mathbf {k} }}}；

其中，單位向量i^{displaystyle {hat {mathbf {i} }}}，j^{displaystyle {hat {mathbf {j} }}}與k^{displaystyle {hat {mathbf {k} }}}分別指向x-軸，y-軸，與z-軸指向的正無窮值方向。

參閱

• 廣義坐標


• 正則坐標


• 平行座標


• 象限角


• 卦限


• 正交坐標系

參考文獻

參考目錄

• 
  Morse PM, Feshbach H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill. 1953: p. 656. ISBN 978-0-07-043316-8.  引文格式1维护：冗余文本 (link)
  

• 
  Margenau H, Murphy GM. The Mathematics of Physics and Chemistry. New York: D. van Nostrand. 1956: p. 177.  引文格式1维护：冗余文本 (link)
  

• 
  Korn GA, Korn TM. Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. 1961: pp. 55–79. ASIN B0000CKZX7.  引文格式1维护：冗余文本 (link)
  

• 
  Sauer R, Szabó I. Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. 1967: p. 94.  引文格式1维护：冗余文本 (link)
  

• 
  Moon P, Spencer DE. Rectangular Coordinates (x, y, z). Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions corrected 2nd ed., 3rd print ed. New York: Springer-Verlag. 1988: pp. 9–11 (Table 1.01). ISBN 978-0387184302.  引文格式1维护：冗余文本 (link)
  

外部連結

• 直角坐標系


• 直角坐標圖的印表


• 
  PlanetMath上直角坐標系的資料。


• MathWorld的直角坐標系