Agfdhyk

函數 f(x)=x2{displaystyle f(x)=x^{2}} 的圖形。

@media all and (max-width:720px){body.skin-minerva .mw-parser-output div.mw-graph{min-width:auto!important;max-width:100%;overflow-x:auto;overflow-y:visible}}

sin(x)等函數的圖形。

在数学中，函数 f 的图形（或图像）指的是所有有序对(x, f(x))组成的集合。具体而言，如果x为实数，则函数图形在平面直角坐标系上呈现为一条曲线。如果函数自变量x为两个实数组成的有序对(x₁, x₂)，则图形就是所有三重序(x₁, x₂, f(x₁, x₂))组成的集合，呈现为曲面（参见三维计算机图形）。

实函数的图形拥有其唯一的图像。而对于一般的函数，其图形形式无法应用，图形的正式定义取决于数学表述的需要，例如泛函分析中的閉圖像定理。

函数图形的概念由二元关系图形推广而来。需要注意的是，尽管一个函数与其图像通常是一一对应的，但二者并不可混淆。两个函数可能拥有相同的图像，却有不同的上域（陪域）。例如，对于下文提到的三次多项式，当其上域为实数时函数即为满射，而若其上域为复数则不然。

通过垂线测试可以判断一条曲线是否为一个函数，而通过水平線測試可以判断函数是否为单射且是否存在反函数。如果反函数存在，则其图像可以通过将原函数图像以直线y=x为轴进行对称得到。

样例

单变量函数

一次函数

三個線性函數的圖形都是直線。紅色與藍色直線的斜率相同。 紅色與綠色直線的 y-截距相同。

形如

f(x)=kx+b {displaystyle f(x)=kx+b! }

的图像为：

{(x,kx+b)|x∈R}{displaystyle left{(x,kx+b)|xin mathbb {R} right}}

在平面直角坐标系中，该图像为一条直线。这是因为，该函数的导数为常数k{displaystyle k}。

非線性函數

函数 f(x)=x3−9x{displaystyle f(x)=x^{3}-9x} 的图像。

对于二次或更高次的多項式函数，或者其他的非線性函數，其图像则会呈现为一条曲线。这是因为其導函數不是常數函數。

例如，三次函数

f(x)=x3−9x {displaystyle f(x)={{x^{3}}-9x}! }

的图像为

{(x,x3−9x)|x∈R}{displaystyle left{(x,x^{3}-9x)|xin mathbb {R} right}}

如果將这个图像绘制在平面直角坐标系中，则会得到一条三次曲线（见右图）。

双变量函数

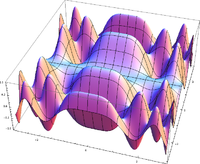
函数 f(x,y)=sin⁡(x2)×cos⁡(y2){displaystyle {begin{smallmatrix}f(x,y)=sin(x^{2})times cos(y^{2})end{smallmatrix}}} 的图像。

三角学中的函数

f(x,y)=sin⁡x2cos⁡y2{displaystyle f(x,y)=sin x^{2}cos y^{2}}

的图像为

{(x,y,sin⁡x2cos⁡y2)|x,y∈R}{displaystyle left{(x,y,sin x^{2}cos y^{2})|x,yin mathbb {R} right}}

如果这个图像绘制在了三维坐标系中，则会得到一个曲面（见图）。

函数图像绘制工具

硬件

TI-83繪圖計算器。

• 图形计算器


• 示波器

软件

参考文献

• Weisstein, Eric W. "Function Graph - MathWorld."

相关条目

维基共享资源中相关的多媒体资源：函数图形

• 函数


• 导数


• 驻点


• 斜率


• 截距


• 方程


• 坐標系