Linear function
In mathematics, the term linear function refers to two distinct but related notions:[1]
- In calculus and related areas, a linear function is a function whose graph is a straight line, that is a polynomial function of degree at most one.[2]
- In linear algebra, mathematical analysis[3], and functional analysis, a linear function is a linear map.[4] In this case, and in case of possible ambiguity, the name affine function is often used for the concept above.[5]
Contents
1 As a polynomial function
2 As a linear map
3 See also
4 Notes
5 References
6 External links
As a polynomial function
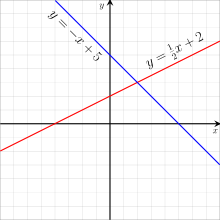
Graphs of two linear (polynomial) functions.
In calculus, analytic geometry and related areas, a linear function is a polynomial of degree one or less, including the zero polynomial (the latter not being considered to have degree zero).
When the function is of only one variable, it is of the form
- f(x)=ax+b,{displaystyle f(x)=ax+b,}
where a and b are constants, often real numbers. The graph of such a function of one variable is a nonvertical line. a is frequently referred to as the slope of the line, and b as the intercept.
For a function f(x1,…,xk){displaystyle f(x_{1},ldots ,x_{k})}
f(x1,…,xk)=b+a1x1+…+akxk{displaystyle f(x_{1},ldots ,x_{k})=b+a_{1}x_{1}+ldots +a_{k}x_{k}},
and the graph is a hyperplane of dimension k.
A constant function is also considered linear in this context, as it is a polynomial of degree zero or is the zero polynomial. Its graph, when there is only one independent variable, is a horizontal line.
In this context, the other meaning (a linear map) may be referred to as a homogeneous linear function or a linear form. In the context of linear algebra, this meaning (polynomial functions of degree 0 or 1) is a special kind of affine map.
As a linear map

The integral of a function is a linear map from the vector space of integrable functions to the real numbers.
In linear algebra, a linear function is a map f between two vector spaces that preserves vector addition and scalar multiplication:
- f(x+y)=f(x)+f(y){displaystyle f(mathbf {x} +mathbf {y} )=f(mathbf {x} )+f(mathbf {y} )}
- f(ax)=af(x).{displaystyle f(amathbf {x} )=af(mathbf {x} ).}
Here a denotes a constant belonging to some field K of scalars (for example, the real numbers) and x and y are elements of a vector space, which might be K itself.
Some authors use "linear function" only for linear maps that take values in the scalar field;[6] these are also called linear functionals.
The "linear functions" of calculus qualify as "linear maps" when (and only when) f([0,…,0])=0{displaystyle f([0,ldots ,0])=0}![{displaystyle f([0,ldots ,0])=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99b368a3b1a4733544e0d4d1a55d70d6f4e04dea)

See also
- Homogeneous function
- Nonlinear system
- Piecewise linear function
- Linear interpolation
- Discontinuous linear map
Notes
^ "The term linear function means a linear form in some textbooks and an affine function in others." Vaserstein 2006, p. 50-1
^ Stewart 2012, p. 23
^ T. M. Apostol (1981). Mathematical Analysis. Addison-Wesley. p. 345..mw-parser-output cite.citation{font-style:inherit}.mw-parser-output q{quotes:"""""""'""'"}.mw-parser-output code.cs1-code{color:inherit;background:inherit;border:inherit;padding:inherit}.mw-parser-output .cs1-lock-free a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-lock-limited a,.mw-parser-output .cs1-lock-registration a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-lock-subscription a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration{color:#555}.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration span{border-bottom:1px dotted;cursor:help}.mw-parser-output .cs1-hidden-error{display:none;font-size:100%}.mw-parser-output .cs1-visible-error{font-size:100%}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-format{font-size:95%}.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-right{padding-right:0.2em}
^ Shores 2007, p. 71
^ A. Kurosh (1975). Higher Algebra. Mir Publishers. p. 214.
^ Gelfand 1961
References
- Izrail Moiseevich Gelfand (1961), Lectures on Linear Algebra, Interscience Publishers, Inc., New York. Reprinted by Dover, 1989.
ISBN 0-486-66082-6
- Thomas S. Shores (2007), Applied Linear Algebra and Matrix Analysis, Undergraduate Texts in Mathematics, Springer.
ISBN 0-387-33195-6
- James Stewart (2012), Calculus: Early Transcendentals, edition 7E, Brooks/Cole.
ISBN 978-0-538-49790-9
- Leonid N. Vaserstein (2006), "Linear Programming", in Leslie Hogben, ed., Handbook of Linear Algebra, Discrete Mathematics and Its Applications, Chapman and Hall/CRC, chap. 50.
ISBN 1-584-88510-6



