Agfdhyk

量纲，又叫作因次（Fundamental unit），是表示一个物理量由基本量组成的情况。确定若干个基本量后，每个导出量都可以表示为基本量的幂的乘积的形式。引入量纲这一概念可以进行量纲分析，这既是物理学的基础，又有着很多重要应用。

由来

物理学中，不同的物理量有着不同的单位，然而这些单位之间都有相互的联系。实际上，恰当地规定一些基本的单位（称为基本单位），可以使任何其他的单位（称为导出单位）都表达为这些单位的乘积，将其统一以便于研究各个物理量之间的關係。如在国际单位制中，功的单位焦耳（J{displaystyle mathrm {J} }），可以表示为“千克平方米每平方秒”（kg⋅m2/s2{displaystyle mathrm {kgcdot m^{2}/s^{2}} }）。

然而，仅仅用单位来表示会面临一些问题：

1. 在不同的单位制下，各个物理量用单位来表示也会不同，以至于起不到预期的“统一各单位”的效果。如英里每小时（mph）与米每秒（m/s）乍看之下无甚联系，然而它们却都是表示速度的单位。虽然说经过转换可以将各个基本单位也统一，然而这样终究不够直观，需记忆也不甚方便，而且选择哪一个单位作为统一单位似乎都不甚公平。


2. 把一个既有的单位表达为拆分了的基本单位的形式实际上没有任何意义，功的单位无论如何都不是“千克二次方米每二次方秒”，因为实际上这个单位根本不存在，它只是与“焦耳”恰好相等而已。况且，这样做也会导致一些拆分后相同但实质不同的单位被混淆，如力矩的单位牛米（N⋅m{displaystyle mathrm {Ncdot m} }）被拆分后也是kg⋅m2/s2{displaystyle mathrm {kgcdot m^{2}/s^{2}} }，然而它与功显然是完全不同的。

因此量纲被作为表达导出单位组成的专有方式引入物理学中。

表示方法

将一个物理导出量用若干个基本量的幂之积表示出来的表达式，称为该物理量的量纲乘积式或量纲式，亦简称量纲。

规定七个基本物理量，在量纲中分别用七个字母表示它们的量纲，他们是：长度（L{displaystyle mathrm {L} }），质量（M{displaystyle mathrm {M} }），时间（T{displaystyle mathrm {T} }），电流（I{displaystyle mathrm {I} }），温度（Θ{displaystyle mathrm {Theta } }），物质的量（N{displaystyle mathrm {N} }），发光强度（J{displaystyle mathrm {J} }）。

则对于任意一个物理量A{displaystyle A}，都可以写出下列量纲式：

dim⁡A=LαMβTγIδΘϵNζJη{displaystyle dim A=mathrm {L^{alpha },M^{beta },T^{gamma },I^{delta },Theta ^{epsilon },N^{zeta },J^{eta }} }

等号左边也可以表示为[A]{displaystyle left[Aright]}。

上式右边称为物理量A{displaystyle A}的量纲。其中，αβγδϵζη{displaystyle alpha ,beta ,gamma ,delta ,epsilon ,zeta ,eta }称为量纲指数。在表示时，七个量纲不一定会全部用上。量纲指数为1的可以省略指数，指数为0的可以省略对应量纲；然而，当所有量纲指数皆为0时（称为无量纲），要将量纲记为“1”。

• 对于功，dim⁡W=L2MT−2{displaystyle dim W=mathrm {L^{2}MT^{-2}} }
  

• 对于磁感应强度，dim⁡B=MT−2I−1{displaystyle dim B=mathrm {MT^{-2}I^{-1}} }
  

• 对于弧度，dim⁡θ=1{displaystyle dim theta =mathrm {1} }
  

值得注意的是，虽然物理量的量纲与取什么单位无关，但量纲却只有在一定的单位制下才有意义。^[1]

量纲分析

量纲分析（Dimensional Analysis），又叫因次分析，是20世纪初提出的在物理领域中建立数学模型的一种方法。量纲分析就是在量纲法则的原则下，分析和探求物理量之间关系。

量纲分析的基础是量纲法则。而在深层次运用中，几乎都还会运用到白金漢π定理，以至于有时候把量纲分析直接看作了“运用Π定理进行无量纲化的过程”。^[2]

量纲的乘除计算

对于不同物理量之间乘、除法导出新的物理量，量纲的计算满足数学上的指数计算法则，即：相乘则对应指数相加，相除则对应指数相减。

例如，根据安培力计算公式F=ILB{displaystyle F=ILB}，可导出磁感应强度的量纲，有

dim⁡B=(dim⁡F)(dim⁡I)(dim⁡L)=LMT−2IL=MT−2I−1{displaystyle {begin{aligned}dim B&={dfrac {(dim F)}{(dim I)(dim L)}}\&=mathrm {dfrac {LMT^{-2}}{IL}} \&=mathrm {MT^{-2}I^{-1}} end{aligned}}}

量纲法则

量纲服从的规律称为量纲法则，它有广泛的应用，一般只指出常用的两条：
1.只有量纲相同的物理量，才能彼此相加、相减和相等；
2.指数函数、对数函数和三角函数的宗量应当是量纲1的。
量纲法则是量纲分析的基础。若推出的公式不符合量纲法则，该式必然是错误的。^[3]

π定理

π定理是由白金汉（E.Buckinghan）于1915年提出的一个定理，故又叫作白金汉定理。其内容为：

设影响某现象的物理量数为n{displaystyle n}个，这些物理量的基本量纲为m{displaystyle m}个，则该物理现象可用N=n−m{displaystyle N=n-m}个独立的无量纲数群（准数）关系式表示。

用数学方式表示为：

设n个物理量之间满足函数关系式：

f(X1,X2,⋯,Xn)=0{displaystyle f(X_{1},X_{2},cdots ,X_{n})=0}

其中，X1,X2,⋯,Xn{displaystyle X_{1},X_{2},cdots ,X_{n}}为物理量。共包含有m个基本量纲（m<n）。则上述关系式与下列关系式等价：

F(Π1,Π2,⋯,Πk)=0{displaystyle F(Pi _{1},Pi _{2},cdots ,Pi _{k})=0}

其中k=n−m{displaystyle k=n-m},Π1,Π2,⋯,Πk{displaystyle Pi _{1},Pi _{2},cdots ,Pi _{k}}为无量纲量，F为未知函数关系。

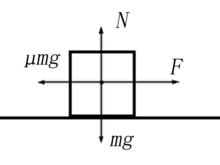
举例：粗糙平面上的一受恒力物体

设在水平面上有一质量为m{displaystyle m}的物体，受一水平力F{displaystyle F}的作用加速滑动，加速度为a{displaystyle a}，物体与水平面之间的滑动摩擦因数为μ{displaystyle mu }，重力加速度大小为g{displaystyle g}。则根据牛顿力学知识，可以写出以下关系式：

F−μmg=ma{displaystyle F-mu mg=ma}

式中有5个物理量，涉及到3个量纲（L{displaystyle mathrm {L} }，M{displaystyle mathrm {M} }，T{displaystyle mathrm {T} }），根据Π定理，这个方程可以由两个无量纲量表示。比如：

Fma−μmgma=1{displaystyle {dfrac {F}{ma}}-{dfrac {mu mg}{ma}}=1}

式中Fma{displaystyle {dfrac {F}{ma}}}与μmgma{displaystyle {dfrac {mu mg}{ma}}}皆为无量纲量，1为常数不加考虑。

于是，原来有五个未知量的式子就被转化为只有两个未知量的了。实际应用当然会比这个复杂得多，然而原理是一样的。

π定理是量纲分析中一个非常重要的定理，它与量纲法则是量纲分析的两大方法，它在建立模型和简化物理过程方面有着巨大的用途。

量纲分析的主要用处

量纲分析是物理学的基础之一，更在空气动力学和流体力学中有重要应用。

• 可以在不同的单位制间进行导出单位的换算。

如，在推导牛顿与达因之间的换算关系时，我们已知dim⁡F=LMT−2{displaystyle dim F=mathrm {LMT^{-2}} }，又知道牛顿使用国际单位制（千克米秒制），达因使用厘米克秒制，1m=100cm，1kg=1000g,于是

1N1dyn=(1m1cm)(1kg1g)(1s1s)−2=105{displaystyle mathrm {{dfrac {1N}{1dyn}}=left({dfrac {1m}{1cm}}right)left({frac {1kg}{1g}}right)left({frac {1s}{1s}}right)^{-2}=10^{5}} }

1N=105dyn{displaystyle mathrm {1N=10^{5}dyn} }

• 验证公式。在对一个公式踌躇不定的时候，可以对等号两边进行取量纲。因为根据量纲的一致性，只有量纲相同的物理量才能进行相加、相减、相等，故可用该方法排除一部分错误。（当然，这并不总是有效。）

比如，对于安培力公式F=ILB{displaystyle F=ILB}，如果不慎记成F=IvB{displaystyle F=IvB}，那么在验证时有，

dim⁡F=LMT−2{displaystyle dim F=mathrm {LMT^{-2}} }

dim⁡IvB=ILT−1MT−2I−1=LMT−3{displaystyle dim IvB=mathrm {ILT^{-1}MT^{-2}I^{-1}=LMT^{-3}} }

显然是不等的，那么便可以得知公式错误；并且还可以知道是少了一个量纲T{displaystyle mathrm {T} }，那么便会更有方向性地寻找错误原因。

• 为复杂公式提供线索，简化复杂物理现象。

比如，对于单摆的周期，我们猜测它可能与单摆的质量m{displaystyle m}、摆长l{displaystyle l}和重力加速度g{displaystyle g}，于是我们假设

T=λmxlygz{displaystyle T=lambda m^{x}l^{y}g^{z}}

其中λ{displaystyle lambda }为常数。两边取量纲，得

T=MxLy(LT−2)z{displaystyle mathrm {T=M^{x}L^{y}(LT^{-2})^{z}} }

根据量纲的一致性，

{0=y+z0=x−2z=1{displaystyle {begin{cases}0=y+z\0=x\-2z=1end{cases}}}

解得x=0，y=0.5，z=-0.5，故

T=λlg{displaystyle T=lambda {sqrt {frac {l}{g}}}}

只需用实验测出λ{displaystyle lambda }的值就可以了。

流体力学中诸如湍流、流体阻力之类的问题，理论非常复杂，有时也常采用实验的方式确定^[4]。我们已经看到，在量纲法则上建立的Π定理把n元关系式简化为n-m元关系式，于是在实际计算中我们只需要这n-m个值便可了解该物理过程了。力学涉及三个量纲（L{displaystyle mathrm {L} }，M{displaystyle mathrm {M} }，T{displaystyle mathrm {T} }），因此通过无量纲化便减少了3个未知量，这实际上大大地简化了实验过程和理论计算。^[5]

參見條目

• 量綱分析

参考文献

书目

脚注