Brillouin zone

The reciprocal lattices (dots) and corresponding first Brillouin zones of (a) square lattice and (b) hexagonal lattice.
In mathematics and solid state physics, the first Brillouin zone is a uniquely defined primitive cell in reciprocal space. In the same way the Bravais lattice is divided up into Wigner–Seitz cells in the real lattice, the reciprocal lattice is broken up into Brillouin zones. The boundaries of this cell are given by planes related to points on the reciprocal lattice. The importance of the Brillouin zone stems from the Bloch wave description of waves in a periodic medium, in which it is found that the solutions can be completely characterized by their behavior in a single Brillouin zone.
The first Brillouin zone is the locus of points in reciprocal space that are closer to the origin of the reciprocal lattice than they are to any other reciprocal lattice points (see the derivation of the Wigner-Seitz cell). Another definition is as the set of points in k-space that can be reached from the origin without crossing any Bragg plane. Equivalently, this is the Voronoi cell around the origin of the reciprocal lattice.

k-vectors exceeding the first Brillouin zone (red) do not carry any more information than their counterparts (black) in the first Brillouin zone.
There are also second, third, etc., Brillouin zones, corresponding to a sequence of disjoint regions (all with the same volume) at increasing distances from the origin, but these are used less frequently. As a result, the first Brillouin zone is often called simply the Brillouin zone. (In general, the n-th Brillouin zone consists of the set of points that can be reached from the origin by crossing exactly n − 1 distinct Bragg planes.)
A related concept is that of the irreducible Brillouin zone, which is the first Brillouin zone reduced by all of the symmetries in the point group of the lattice (point group of the crystal).[1]
The concept of a Brillouin zone was developed by Léon Brillouin (1889–1969), a French physicist.
Contents
1 Critical points
2 See also
3 References
4 External links
Critical points

First Brillouin zone of FCC lattice, a truncated octahedron, showing symmetry labels for high symmetry lines and points
Several points of high symmetry are of special interest – these are called critical points.[2]
| Symbol | Description |
|---|---|
| Γ | Center of the Brillouin zone |
| Simple cube | |
| M | Center of an edge |
| R | Corner point |
| X | Center of a face |
| Face-centered cubic | |
| K | Middle of an edge joining two hexagonal faces |
| L | Center of a hexagonal face |
| U | Middle of an edge joining a hexagonal and a square face |
| W | Corner point |
| X | Center of a square face |
| Body-centered cubic | |
| H | Corner point joining four edges |
| N | Center of a face |
| P | Corner point joining three edges |
| Hexagonal | |
| A | Center of a hexagonal face |
| H | Corner point |
| K | Middle of an edge joining two rectangular faces |
| L | Middle of an edge joining a hexagonal and a rectangular face |
| M | Center of a rectangular face |
Other lattices have different types of high-symmetry points. They can be found in the illustrations below.
| Lattice system | Bravais lattice (Abbreviation) | ||||
|---|---|---|---|---|---|
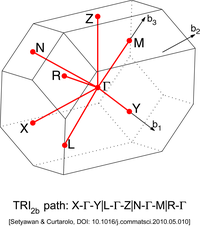
Triclinic | Primitive triclinic (TRI) | Triclinic Lattice type 1a (TRI1a)
| Triclinic Lattice type 1b (TRI1b)
| Triclinic Lattice type 2a (TRI2a)
| Triclinic Lattice type 2b (TRI2b)
|
Monoclinic | Primitive monoclinic (MCL) | Monoclinic Lattice (MCL)
| |||
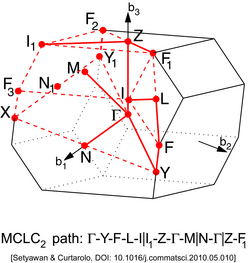
| Base-centered monoclinic (MCLC) | Base Centered Monoclinic Lattice type 1 (MCLC1)
| Base Centered Monoclinic Lattice type 2 (MCLC2)
| Base Centered Monoclinic Lattice type 3 (MCLC3)
| Base Centered Monoclinic Lattice type 4 (MCLC4)
| Base Centered Monoclinic Lattice type 5 (MCLC5)
|
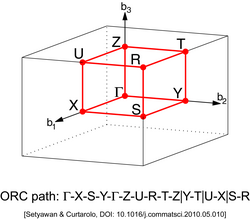
Orthorhombic | Primitive orthorhombic (ORC) | Simple Orthorhombic Lattice (ORC)
| |||
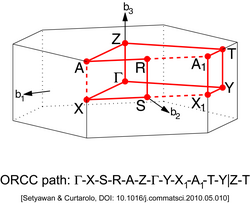
| Base-centered orthorhobmic (ORCC) | Base Centered Orthorhombic Lattice (ORCC)
| ||||
| Body-centered orthorhombic (ORCI) | Body Centered Orthorhombic Lattice (ORCI)
| ||||
| Face-centered orthorhombic (ORCF) | Face Centered Orthorhombic Lattice type 1 (ORCF1)
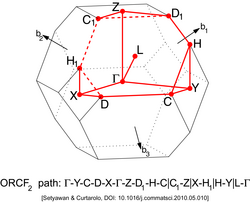
| Face Centered Orthorhombic Lattice type 2 (ORCF2)
| Face Centered Orthorhombic Lattice type 3 (ORCF3)
| ||
Tetragonal | Primitive tetragonal (TET) | Simple Tetragonal Lattice (TET)
| |||
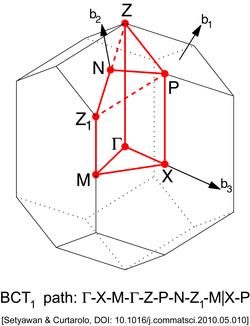
| Body-centered Tetragonal (BCT) | Body Centered Tetragonal Lattice type 1 (BCT1)
| Body Centered Tetragonal Lattice type 2 (BCT2)
| |||
Rhombohedral | Primitive rhombohederal (RHL) | Rhombohedral Lattice type 1 (RHL1)
| Rhombohedral Lattice type 2 (RHL2)
| ||
Hexagonal | Primitive hexagonal (HEX) | Hexagonal Lattice (HEX)
| |||
Cubic | Primitive cubic (CUB) | Simple Cubic Lattice (CUB)
| |||
| Body-centered cubic (BCC) | Body Centered Cubic Lattice (BCC)
| ||||
| Face-centered cubic (FCC) | Face Centered Cubic Lattice (FCC)
|
See also

Brillouin-zone construction by selected area diffraction, using 300 keV electrons.
- Fundamental pair of periods
- Fundamental domain
References
^ Thompson, Nick. "Irreducible Brillouin Zones and Band Structures". bandgap.io. Retrieved 13 December 2017..mw-parser-output cite.citation{font-style:inherit}.mw-parser-output .citation q{quotes:"""""""'""'"}.mw-parser-output .citation .cs1-lock-free a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-limited a,.mw-parser-output .citation .cs1-lock-registration a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-subscription a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration{color:#555}.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration span{border-bottom:1px dotted;cursor:help}.mw-parser-output .cs1-ws-icon a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/4/4c/Wikisource-logo.svg/12px-Wikisource-logo.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output code.cs1-code{color:inherit;background:inherit;border:inherit;padding:inherit}.mw-parser-output .cs1-hidden-error{display:none;font-size:100%}.mw-parser-output .cs1-visible-error{font-size:100%}.mw-parser-output .cs1-maint{display:none;color:#33aa33;margin-left:0.3em}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-format{font-size:95%}.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-right{padding-right:0.2em}
^ Ibach, Harald; Lüth, Hans (1996). Solid-State Physics, An Introduction to Principles of Materials Science (2nd ed.). Springer-Verlag. ISBN 978-3-540-58573-2.
^ Setyawan, Wahyu; Curtarolo, Stefano (2010). "High-throughput electronic band structure calculations: Challenges and tools". Computational Materials Science. 49 (2): 299–312. arXiv:1004.2974. Bibcode:2010arXiv1004.2974S. doi:10.1016/j.commatsci.2010.05.010.
Kittel, Charles (1996). Introduction to Solid State Physics. New York City: Wiley. ISBN 978-0-471-14286-7.
Ashcroft, Neil W.; Mermin, N. David (1976). Solid State Physics. Orlando: Harcourt. ISBN 978-0-03-049346-1.
Brillouin, Léon (1930). "Les électrons dans les métaux et le classement des ondes de de Broglie correspondantes". Comptes Rendus Hebdomadaires des Séances de l'Académie des Sciences. 191 (292).
External links
- Brillouin Zone simple lattice diagrams by Thayer Watkins
- Brillouin Zone 3d lattice diagrams by Technion.
- DoITPoMS Teaching and Learning Package- "Brillouin Zones"
- Aflowlib.org consortium database (Duke University)
- AFLOW Standardization of VASP/QUANTUM ESPRESSO input files (Duke University)